🚩 [ACL 2025] Chain-of-Reasoning: Towards Unified Mathematical Reasoning in Large Language Models via a Multi-Paradigm Perspective
Published in ACL, 2025
关键词
- 多范式 / Multi-Paradigm
- 数学推理 / Mathematical Reasoning
- 大语言模型 / Large Language Model (LLM)
- 逐步训练 / Progressive Paradigm Training (PPT)
- 自然语言推理 / Natural Language Reasoning (NLR)
- 算法推理 / Algorithmic Reasoning (AR)
- 符号推理 / Symbolic Reasoning (SR)
- 零样本泛化 / Zero-shot Generalization
Arxiv地址:https://arxiv.org/abs/2501.11110 ACL 2025:https://aclanthology.org/2025.acl-long.1213/
背景
随着大语言模型(LLM)在数学推理任务上的快速发展,当前的模型通常专注于单一推理范式(如自然语言、代码、或符号推理),导致它们在不同类型的数学任务中表现不均衡。例如,某些模型擅长自然语言推理,但在定理证明等需要符号推理的任务中表现较差,反之亦然。这种“单一范式”的方法不仅限制了模型在各自任务上的上限,也影响了跨任务、跨范式的泛化能力。
为了解决这一挑战,作者提出了“Chain-of-Reasoning(CoR)”框架,通过集成自然语言推理(NLR)、算法推理(AR)和符号推理(SR)三大范式,实现协同推理,提升模型在复杂数学问题上的综合推理能力和泛化能力。
方法
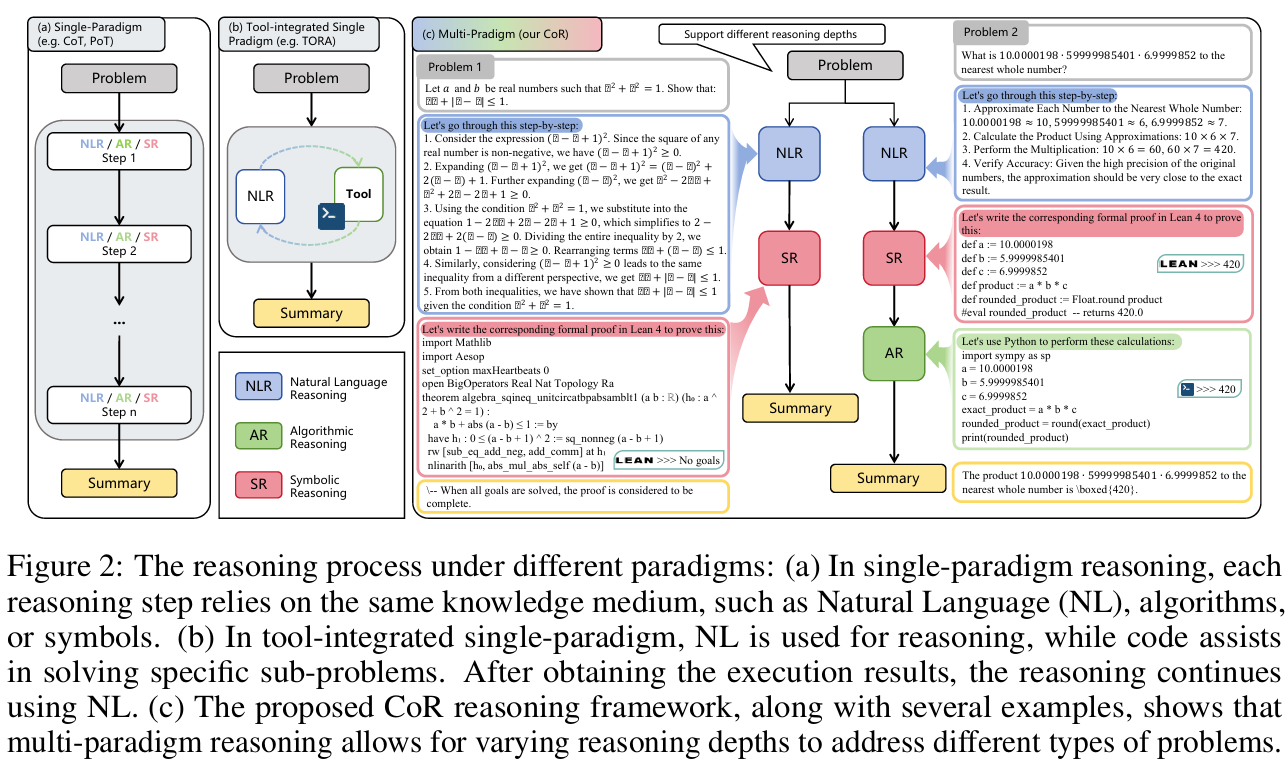
CoR 框架的核心思路与创新:
- 多范式协同推理:
- CoR 不再局限于单一推理方式,而是允许模型在同一问题上依次使用 NLR、AR、SR 等多种推理路径,各自独立生成候选解答后,最后再综合归纳为最终答案。
- 通过在推理过程中动态切换不同范式,实现多视角、多工具的互补,提高推理的全面性和准确性。
- 逐步范式训练(Progressive Paradigm Training, PPT):
- 训练过程中,模型先学会用自然语言解决问题,再逐步引入算法和符号推理的能力,最终综合三者,提升对多种推理范式的掌握和融合能力。
- 训练数据采用作者自构建的大规模多范式数学推理数据集(MPM),涵盖 16.7 万条推理路径。
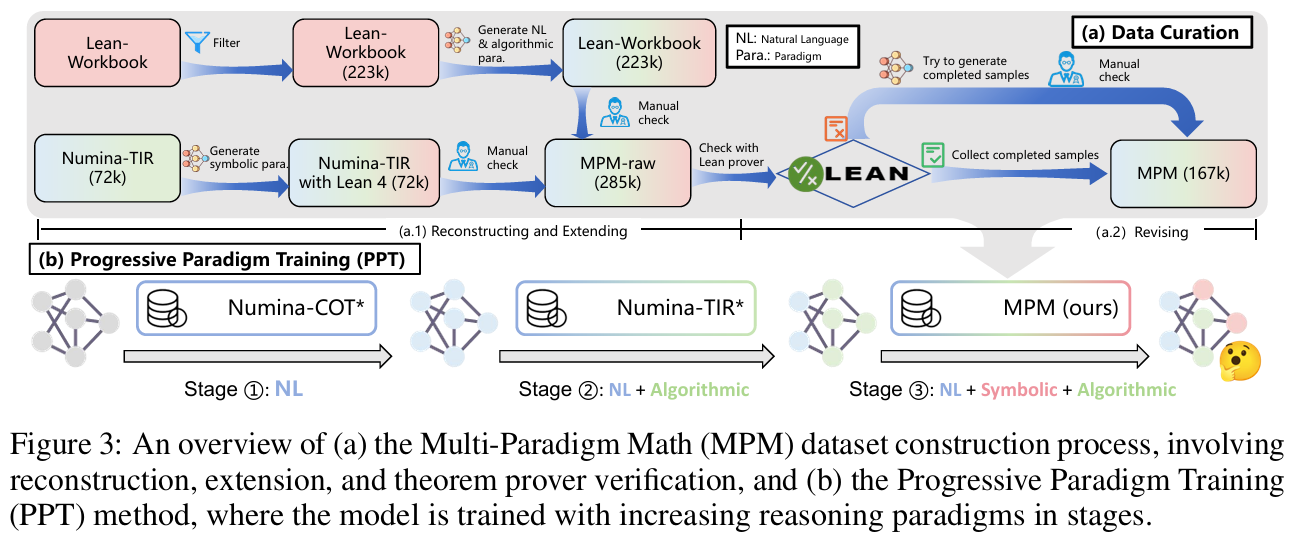

- 推理与采样机制:
- 零样本推理阶段,模型根据任务需求调整推理深度与范式切换顺序。
- 引入“顺序多范式采样(Sequential Multi-Paradigm Sampling, SMPS)”,通过在不同范式间采样推理路径,极大丰富了解题思路和输出的多样性。
讨论
我们认为大语言模型(LLM)推理过程的层级结构,分为三个主要层次:推理范式(Paradigms)、推理路径(Paths)、推理步骤(Steps),以及单一与多范式推理的结构对比。
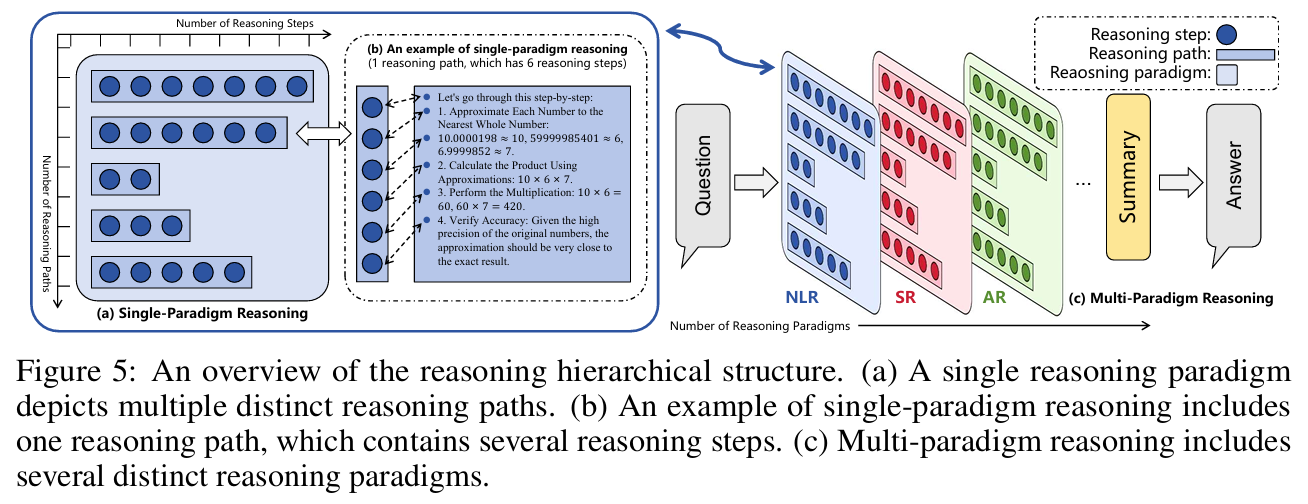
- (a) 单一范式推理(Single-Paradigm Reasoning)
展示在同一推理范式下(如仅自然语言、仅代码、仅符号)的多路径推理过程。- 宽度(width):指不同推理路径的数量。通过采样、打分等方式生成多个独立推理路径(如 Random Sampling、Monte Carlo Search),然后用 Best-of-N、Self-consistency 等整合策略汇总答案。
- 深度(depth):指单一推理路径中推理步骤的数量,如 Chain-of-Thought(CoT)方法通过增加中间步骤提升推理表现。
(b) 单一范式推理示例
给出了一个具体推理路径及其步骤,比如将数值近似后乘积计算,每一步作为一个推理步骤,最终获得答案。- (c) 多范式推理(Multi-Paradigm Reasoning, CoR)
展示多个不同推理范式(NLR:自然语言推理,AR:算法推理,SR:符号推理)协同工作的场景。模型可以在同一问题上串联使用多种推理方式,每种范式独立产出推理路径,再综合得出最终答案。这突破了“仅在单一知识媒介内推理”的限制,大大扩展了解题的空间和能力。
核心要点:
- LLM 推理具备层级性:推理步骤 → 路径 → 范式。
- 传统研究聚焦于单一范式内的宽度或深度优化,而 CoR 首次实现多范式的协同推理。
- 多范式推理允许模型跨多种知识表达方式协作完成复杂任务,提高了泛化能力和表现上限。
下图对比了当前主流研究中的不同推理方法,重点突出了多范式推理 CoR 的创新之处。该图分为三部分:
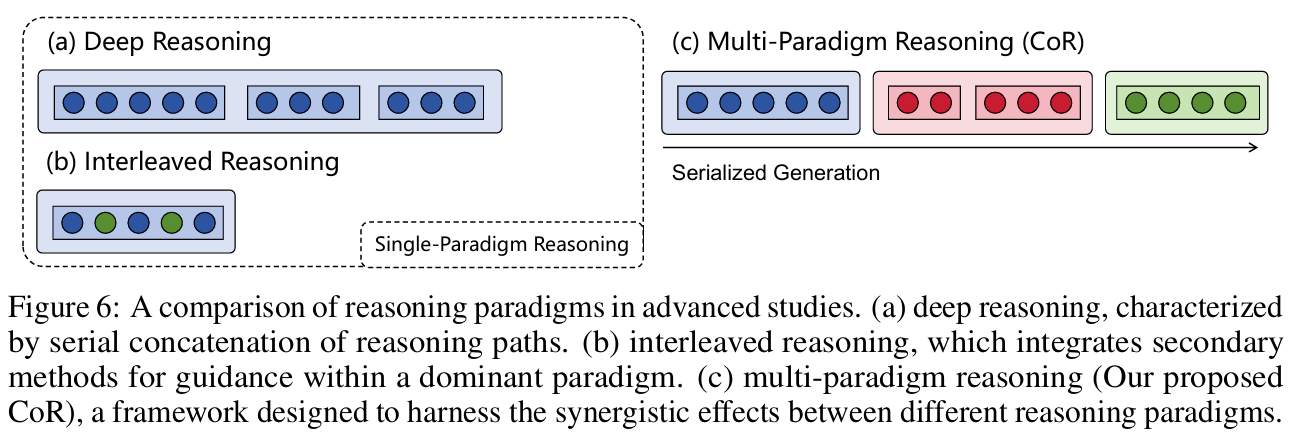
(a) 深度推理(Deep Reasoning)
代表如 OpenAI o1 等工作,专注于在同一推理路径内进行串联推理,通过不断延长推理步骤(depth),最终用摘要模块整合答案。这类方法强调推理链条的深入和详细性,能提升单一路径的推理表现。- (b) 交错推理(Interleaved Reasoning)
如 ToRA、InternLM2.5-StepProver 等,主导范式是自然语言,但中间引入代码生成、执行,或用自然语言辅助符号推理。典型流程为自然语言→代码→自然语言、自然语言→符号→自然语言等。- 这类方法虽然有多种知识媒介的融合,但主导范式可独立完成推理,辅助范式只是起到补充作用。因此仍属于单一范式增强型,而非真正意义上的多范式协同推理。
- (c) 多范式推理(Multi-Paradigm Reasoning, CoR)
强调多种推理范式之间的顺序依赖和协同作用。例如,自然语言推理结果作为输入进一步传递给符号推理或算法推理。每个范式的输出不仅影响后续步骤,还为全局推理提供了基础信息。这一模式使模型具备更高效的推理能力和更强的泛化能力,是测试时扩展推理规模的新方向。
创新意义与优势:
- CoR 不只是“多一步推理”或“多一种工具”,而是多范式的联动、串联,每一范式的结果对下一个范式提供基础和指引。
- 多范式推理不仅拓展了解题空间,还提升了搜索与优化的多样性和深度,为复杂问题的高效求解提供了新的思路。
实验
实验设置:
- 数据集:
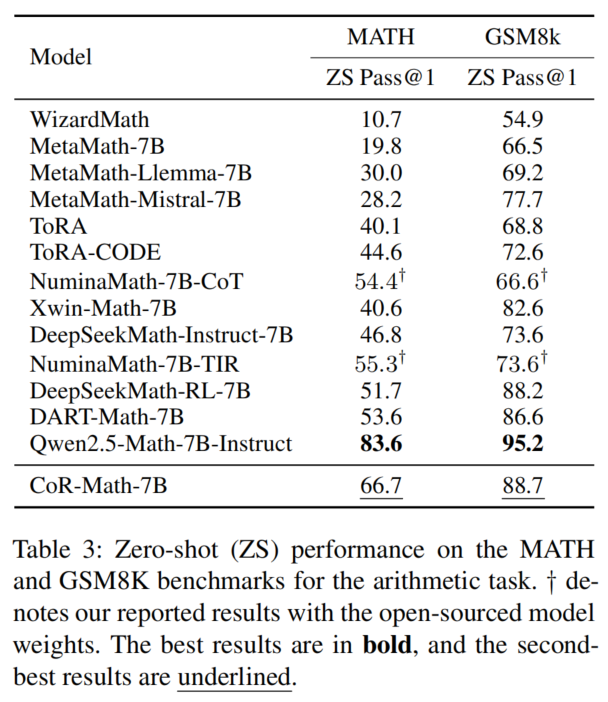
- 算术推理:GSM8K、MATH、AMC2023、AIME2024
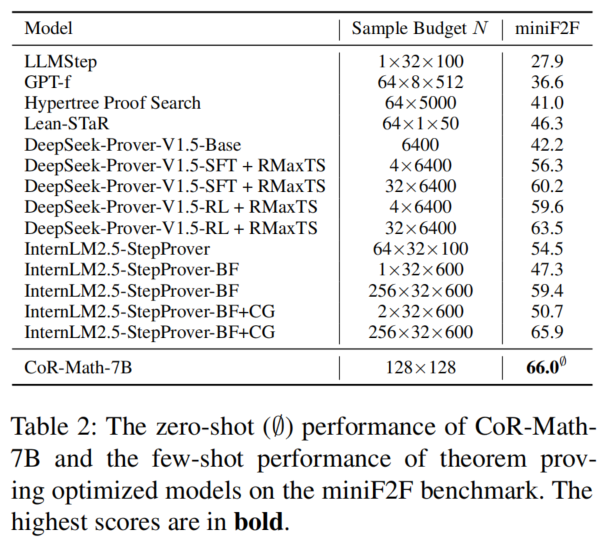
- 定理证明:miniF2F(奥赛级难度)
- 模型训练:
- 基于 DeepSeekMath-Base-7B 和 Llama-3.1-8B 进行微调。
- 按照 PPT 方法,分阶段逐步扩展范式(NLR → NLR+AR → NLR+AR+SR)。
- 评测指标:
- 主指标为准确率(Accuracy)。对于定理证明,采用 pass@N 评估不同采样次数下的正确率。
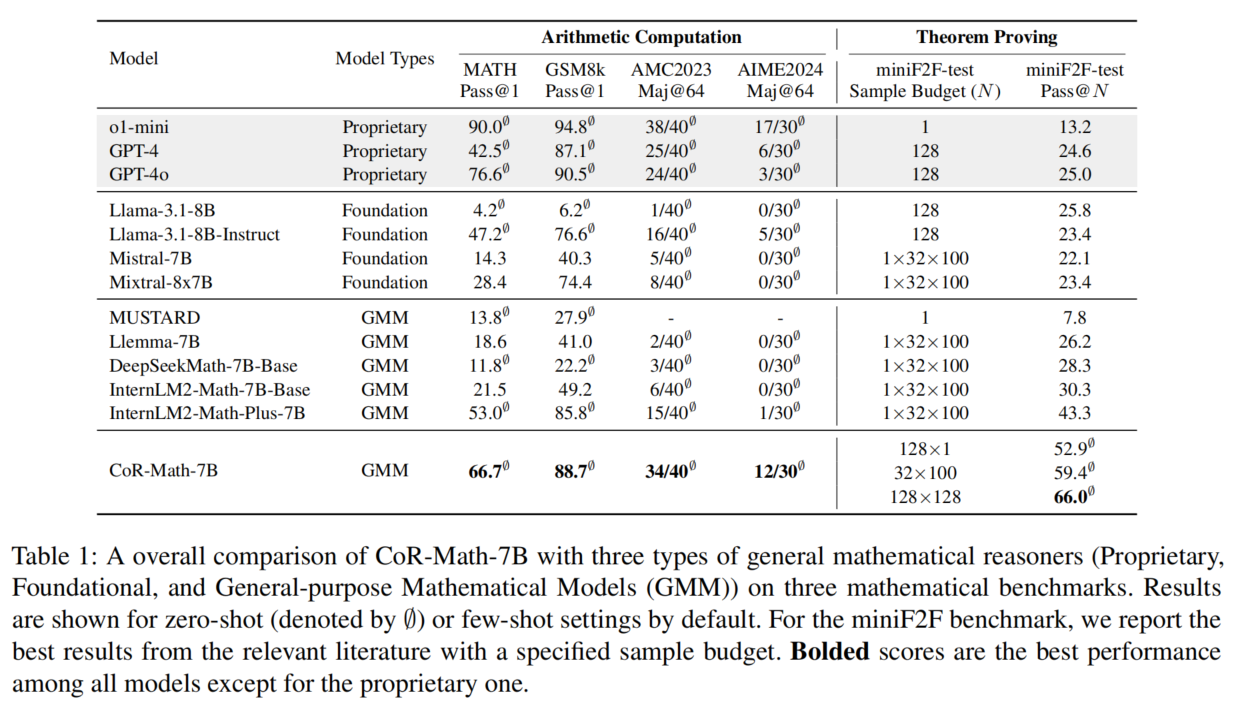
- 对比基线:
- 泛用数学模型:如 GPT-4、Llama-3、InternLM2-Math、MetaMath 等。
- 专家模型:如 DeepSeek-Prover、WizardMath、ToRA 等。
结果
主要结果总结:
- 综合性能提升显著:
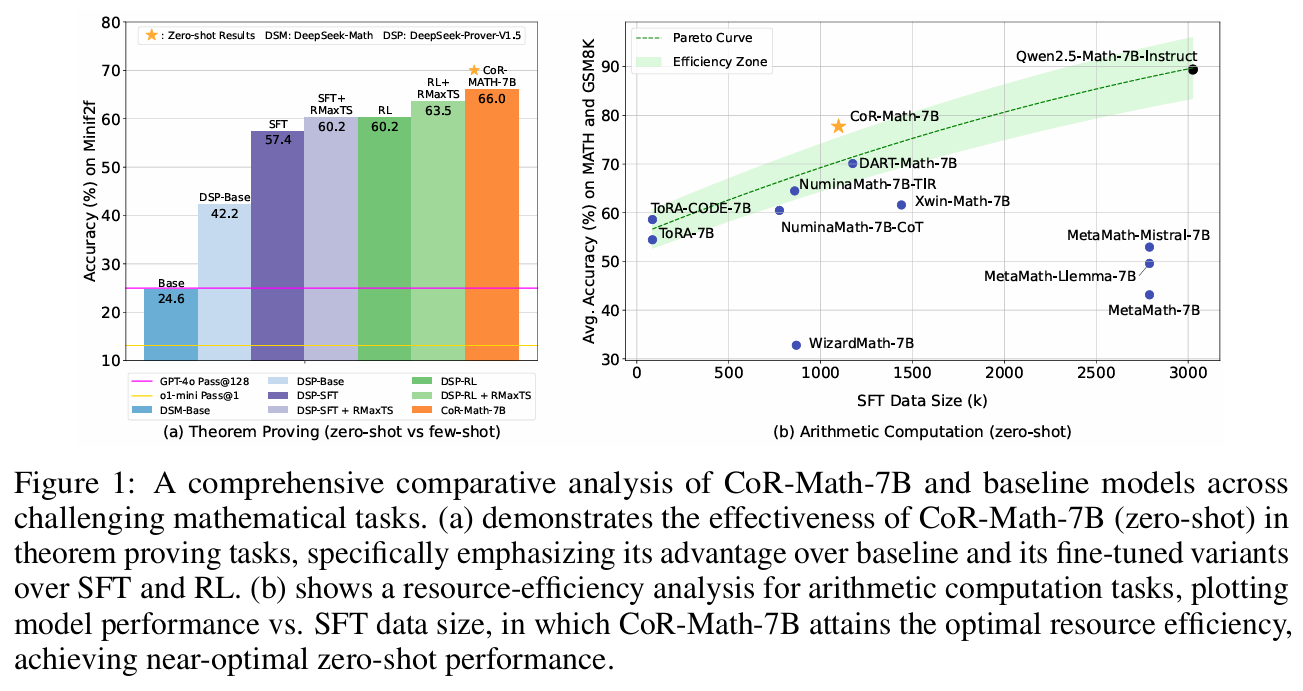
- CoR-Math-7B 在五个主流基准上全面超越当前 SOTA,特别是在零样本设定下效果突出。
- 定理证明任务 miniF2F 上,零样本准确率比 GPT-4o 提升 41.0%,超越所有 few-shot 专家模型。
- 算术任务 MATH 上,较强基线(如 RL-based 方法)提升高达 15%。
- 资源利用与泛化:
- 在数据量相近条件下,CoR-Math-7B 的表现突破了“单范式方法”的最优表现曲线,展示了更优的效率与能力。
- 逐步训练(PPT)有效促进了模型对多种范式的逐步掌握和协同提升。
- 消融实验与机制验证:
- 多范式协同推理相比单一范式微调,带来了显著的跨任务、跨难度提升。
- 推理范式顺序也影响最终效果,例如先符号后算法推理比反之更优。
总结
本论文提出的 Chain-of-Reasoning(CoR)是面向大语言模型数学推理的新一代统一框架,通过集成自然语言、算法、符号三种推理范式,实现了在算术、定理证明等多类任务上的协同提升和高效零样本泛化。提出的逐步范式训练策略和多范式数据集,为 LLM 数学推理能力的突破提供了方法论和实践样例。实验证明,该方法显著超越目前主流开源与专有模型,为今后智能体多范式推理研究与应用奠定了坚实基础。